Young87

SmartCat's Blog

So happy to code my life!

游戏开发交流QQ群号60398951

当前位置：首页 >跨站数据测试

ADT: Disjoint Set 并查集（不相交集合）（Java 实现）

日期： 2020-12-11    分类： 跨站数据测试 645次阅读

ADT: Disjoint Set 并查集（不相交集合）（Java 实现）

文章目录

简介

本篇来介绍并查集(disjoint-set)。很多时候我们会遇到这样一个场景，我们需要将许多各元素按照某种规则进行分类（也可以说是所谓的划分），我们可以举几个例子说明：

  • 围棋游戏
    在围棋游戏中每个棋子是一个元素，则连在一起的棋子就应当被划分在同一个集合之内；

  • 无向图的强连通集(Strong Connected Components)
    强连通集表示可经过任意路径长相互抵达的节点属于同一个连通集，则在这个场景图节点是元素，而连通集表示集合

再多的例子我现在也想不到了。然而在实现的时候我们反过来，利用合并(union)操作将分散的元素组合到一个集合之内。马上就来看看并查集是如何实现吧！（使用森林的实现方式，语言采用 Java）

参考

算法导论（原书第三版）

正文

抽象接口描述

首先我们先定义并查集(disjoint-set)的抽象接口：

MAKE-SET(x)
建立集合：根据元素 x 建立新的集合
UNION(x, y)
合并集合：将元素 x 和元素 y 所属的集合合并
FIND-SET(x)
查找集合：查找元素 x 所属的集合（返回集合代表元素）

并查集的主要操作就是以上三种，接下来我们来看看实现

基本 Java 实现

相关实现说明可以参照下方代码内注释，实现出的抽象对象节点关系可能如下图所示：

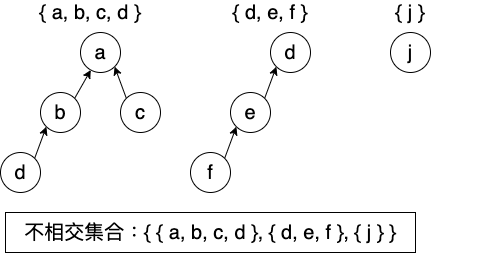
接口定义

  • DisjointSet.java
package adt.disjointset;

/**
 * 并查集（不相交集合）
 * @param <T>
 */
public interface DisjointSet<T> {

    /**
     * 建立新的集合
     * @param t
     * @return
     */
    boolean create(T t);

    /**
     * 合并集合
     */
    boolean union(T x, T y);

    /**
     * 查找集合
     */
    T find(T x);

    /**
     * 返回集合数量
     */
    int size();

    /**
     * 检查两个元素是否属于同一个集合
     */
    default boolean same(T x, T y) {
        return find(x) == find(y);
    }
}

具体实现类

  • DisjointSetForest.java
package adt.disjointset;

import java.util.*;

/**
 * 并查集森林（每个集合为一棵树）实现
 */
public class DisjointSetForest<T> implements DisjointSet<T> {

    /**
     * 内部树节点类
     *
     * @param <T>
     */
    private static class Node<T> {
        T t;
        Node<T> p;

        Node(T t) {
            this.t = t;
            // 代表元素的父节点指针指向自己
            this.p = this;
        }
    }

    /**
     * 保存所有集合的根节点
     */
    private List<Node<T>> forest;
    /**
     * 保存值到节点的映射
     */
    private Map<T, Node<T>> mapper;

    DisjointSetForest() {
        forest = new LinkedList<>();
        mapper = new HashMap<>();
    }

    DisjointSetForest(List<T> initialSets) {
        forest = new LinkedList<>();
        mapper = new HashMap<>();
        for (T t : initialSets) {
            // 初始化时每个元素自己为一个集合
            Node<T> n = new Node<>(t);
            forest.add(n);
            mapper.put(t, n);
        }
    }

    @Override
    public boolean create(T t) {
        // 创建新的集合（作为根节点，即代表元素），并分别加入到两个表中
        Node<T> n = new Node<>(t);
        mapper.put(t, n);
        return forest.add(n);
    }

    @Override
    public boolean union(T x, T y) {
        Node<T> n1 = findNode(x);
        Node<T> n2 = findNode(y);
        if (n1 == null || n2 == null) return false;
        // 合并两个集合即使一个集合的代表元素指向另一个集合的代表元素
        n2.p = n1;
        return true;
    }

    @Override
    public T find(T x) {
        Node<T> n = findNode(x);
        return n == null ? null : n.t;
    }

    private Node<T> findNode(T x) {
        Node<T> n = mapper.get(x);
        if (n == null) {
            return null;
        }
        // 不断找父节点直到根节点即代表元素
        while (n != n.p) {
            n = n.p;
        }
        return n;
    }

    @Override
    public int size() {
        // 集合数量即根节点（代表元素）的数量
        return forest.size();
    }

    @Override
    public String toString() {
        Map<T, List<T>> sets = new HashMap<>();
        for (T t : mapper.keySet()) {
            T root = find(t);
            if (!sets.containsKey(root)) {
                sets.put(root, new ArrayList<>());
            }
            sets.get(root).add(t);
        }
        StringBuilder res = new StringBuilder();
        for (T present : sets.keySet()) {
            res.append(present);
            res.append(":");
            res.append(sets.get(present));
            res.append("\n");
        }
        return res.toString();
    }
}

在具体实现中我们定义了一个内部节点类(Node)作为集合树的内部节点，并保存一个元素到节点的映射表(mapper)

测试

  • DisjointSetTest.java
package adt.disjointset;
import org.junit.Test;
import java.util.Arrays;
import static org.junit.Assert.*;

public class DisjointSetTest {

    /**
     * {{1, 2, 3}, {4}, {0, 5}}
     */
    @Test
    public void test_1() {
        Integer[] nums = new Integer[]{0, 1, 2, 3, 4, 5};
        DisjointSet<Integer> set = new DisjointSetForest<>(Arrays.asList(nums));
        set.union(0, 5);
        set.union(1, 2);
        set.union(2, 3);
        System.out.println(set);
        // {0, 5}
        assertEquals(true, set.same(0, 0));
        assertEquals(false, set.same(0, 1));
        assertEquals(false, set.same(0, 2));
        assertEquals(false, set.same(0, 3));
        assertEquals(false, set.same(0, 4));
        assertEquals(true, set.same(0, 5));
        // {1, 2, 3}
        assertEquals(false, set.same(2, 0));
        assertEquals(true, set.same(2, 1));
        assertEquals(true, set.same(2, 2));
        assertEquals(true, set.same(2, 3));
        assertEquals(false, set.same(2, 4));
        assertEquals(false, set.same(2, 5));
        // {4}
        assertEquals(false, set.same(4, 0));
        assertEquals(false, set.same(4, 1));
        assertEquals(false, set.same(4, 2));
        assertEquals(false, set.same(4, 3));
        assertEquals(true, set.same(4, 4));
        assertEquals(false, set.same(4, 5));
    }

    /**
     * {{a, b, c, d}, {e, f, g}, {h, i}, {j}}
     */
    @Test
    public void test_2() {
        Character[] chars = new Character[]{'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'};
        DisjointSet<Character> set = new DisjointSetForest<>(Arrays.asList(chars));
        set.union(chars[0], chars[1]);
        set.union(chars[0], chars[2]);
        set.union(chars[0], chars[3]);
        set.union(chars[4], chars[5]);
        set.union(chars[4], chars[6]);
        set.union(chars[7], chars[8]);
        System.out.println(set);
        // {a, b, c, d}
        assertEquals(true, set.same(chars[2], chars[0]));
        assertEquals(true, set.same(chars[2], chars[1]));
        assertEquals(true, set.same(chars[2], chars[2]));
        assertEquals(true, set.same(chars[2], chars[3]));
        assertEquals(false, set.same(chars[2], chars[4]));
        assertEquals(false, set.same(chars[2], chars[5]));
        assertEquals(false, set.same(chars[2], chars[6]));
        assertEquals(false, set.same(chars[2], chars[7]));
        assertEquals(false, set.same(chars[2], chars[8]));
        assertEquals(false, set.same(chars[2], chars[9]));
        // {e, f, g}
        assertEquals(false, set.same(chars[6], chars[0]));
        assertEquals(false, set.same(chars[6], chars[1]));
        assertEquals(false, set.same(chars[6], chars[2]));
        assertEquals(false, set.same(chars[6], chars[3]));
        assertEquals(true, set.same(chars[6], chars[4]));
        assertEquals(true, set.same(chars[6], chars[5]));
        assertEquals(true, set.same(chars[6], chars[6]));
        assertEquals(false, set.same(chars[6], chars[7]));
        assertEquals(false, set.same(chars[6], chars[8]));
        assertEquals(false, set.same(chars[6], chars[9]));
        // {h, i}
        assertEquals(false, set.same(chars[8], chars[0]));
        assertEquals(false, set.same(chars[8], chars[1]));
        assertEquals(false, set.same(chars[8], chars[2]));
        assertEquals(false, set.same(chars[8], chars[3]));
        assertEquals(false, set.same(chars[8], chars[4]));
        assertEquals(false, set.same(chars[8], chars[5]));
        assertEquals(false, set.same(chars[8], chars[6]));
        assertEquals(true, set.same(chars[8], chars[7]));
        assertEquals(true, set.same(chars[8], chars[8]));
        assertEquals(false, set.same(chars[8], chars[9]));
        // {j}
        assertEquals(false, set.same(chars[9], chars[0]));
        assertEquals(false, set.same(chars[9], chars[1]));
        assertEquals(false, set.same(chars[9], chars[2]));
        assertEquals(false, set.same(chars[9], chars[3]));
        assertEquals(false, set.same(chars[9], chars[4]));
        assertEquals(false, set.same(chars[9], chars[5]));
        assertEquals(false, set.same(chars[9], chars[6]));
        assertEquals(false, set.same(chars[9], chars[7]));
        assertEquals(false, set.same(chars[9], chars[8]));
        assertEquals(true, set.same(chars[9], chars[9]));
    }
}

输出

2:[1, 2, 3]
4:[4]
5:[0, 5]

b:[a, b, c, d]
f:[e, f, g]
i:[h, i]
j:[j]

操作优化

到此我们已经实现了基本的并查集操作了，可以创建、合并、查找集合。接下来我们可以使用两种实现非常简单的技术来优化并查集的操作：按秩合并 & 路径压缩

按秩合并

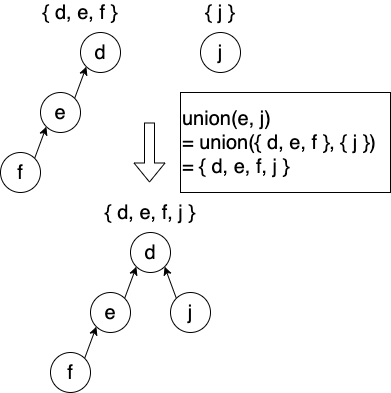
第一个优化是针对合并(union)操作，我们发现整个集合运行的过程只有在合并集合的时候才会使树的高度增加。按秩合并便是希望使树高度的增加最小化，为此我们需要修改原本实现的两个地方：

核心思想：将较矮的集合作为子节点

private static class Node<T> {
    T t;
    Node<T> p;
    int depth; // 保存该节点深度

    Node(T t) {
        this.t = t;
        this.p = this;
        depth = 1;
    }
}

public boolean union(T x, T y) {
    Node<T> n1 = findNode(x);
    Node<T> n2 = findNode(y);
    if (n1 == null || n2 == null) return false;
    // 将较矮的集合合并到较高的集合
    if (n1.depth > n2.depth) {
        n2.p = n1;
    } else {
        n1.p = n2;
        // 只有两个集合高度相同的时候合并后高度才会递增
        if (n1.depth == n2.depth) {
            n2.depth++;
        }
    }
    return true;
}

路径压缩

第二个优化是针对搜索(find)的优化，我们发现，如果一次经过大量的合并操作会使得集合的树高不断增加，即便有按秩合并仍有可能产生非常深的树结构。路径压缩的思想便是每次搜索集合代表元素的时候，将路径上所有元素的父指针直接指向代表元素，这将会大大减少下次搜索代表元素的时间。

核心思想：使搜索时路径上所有元素直接指向代表元素

public T find(T x) {
    Node<T> n = findNode(x);
    return n == null ? null : n.t;
}

private Node<T> findNode(T x) {
    Node<T> n = mapper.get(x);
    if (n == null) {
        return null;
    }
    return findNode(n);
}

/**
 * 带路径压缩的搜索
 *
 * @param n
 * @return
 */
private Node<T> findNode(Node<T> n) {
    if (n != n.p) {
        n.p = findNode(n.p); // 递归回溯（findNode 返回代表元素）
    }
    return n.p;
}

透过修改 findNode 的实现，并应用递归回溯的特性来完成路径压缩

完整 Java 实现（带按秩合并和路径压缩）

最终附上实现优化之后的完整代码：

  • DisjointSet.java
package adt.disjointset;

/**
 * 并查集（不相交集合）
 * @param <T>
 */
public interface DisjointSet<T> {

    /**
     * 建立新的集合
     * @param t
     * @return
     */
    boolean create(T t);

    /**
     * 合并集合
     */
    boolean union(T x, T y);

    /**
     * 查找集合
     */
    T find(T x);

    /**
     * 返回集合数量
     */
    int size();

    /**
     * 检查两个元素是否属于同一个集合
     */
    default boolean same(T x, T y) {
        return find(x) == find(y);
    }
}
  • DisjointSetForest.java
package adt.disjointset;

import java.util.*;

/**
 * 并查集森林（每个集合为一棵树）实现
 */
public class DisjointSetForest<T> implements DisjointSet<T> {

    /**
     * 内部树节点类
     *
     * @param <T>
     */
    private static class Node<T> {
        T t;
        Node<T> p;
        int depth;

        Node(T t) {
            this.t = t;
            this.p = this;
            depth = 1;
        }
    }

    /**
     * 保存所有集合的根节点
     */
    private List<Node<T>> forest;
    /**
     * 保存值到节点的映射
     */
    private Map<T, Node<T>> mapper;

    DisjointSetForest() {
        forest = new LinkedList<>();
        mapper = new HashMap<>();
    }

    DisjointSetForest(List<T> initialSets) {
        forest = new LinkedList<>();
        mapper = new HashMap<>();
        for (T t : initialSets) {
            Node<T> n = new Node<>(t);
            forest.add(n);
            mapper.put(t, n);
        }
    }

    @Override
    public boolean create(T t) {
        Node<T> n = new Node<>(t);
        mapper.put(t, n);
        return forest.add(n);
    }

    /**
     * 按秩合并
     *
     * @param x
     * @param y
     * @return
     */
    @Override
    public boolean union(T x, T y) {
        Node<T> n1 = findNode(x);
        Node<T> n2 = findNode(y);
        if (n1 == null || n2 == null) return false;
        if (n1.depth > n2.depth) {
            n2.p = n1;
        } else {
            n1.p = n2;
            if (n1.depth == n2.depth) {
                n2.depth++;
            }
        }
        return true;
    }

    @Override
    public T find(T x) {
        Node<T> n = findNode(x);
        return n == null ? null : n.t;
    }

    private Node<T> findNode(T x) {
        Node<T> n = mapper.get(x);
        if (n == null) {
            return null;
        }
        return findNode(n);
    }

    /**
     * 带路径压缩的搜索
     *
     * @param n
     * @return
     */
    private Node<T> findNode(Node<T> n) {
        if (n != n.p) {
            n.p = findNode(n.p);
        }
        return n.p;
    }

    @Override
    public int size() {
        return forest.size();
    }

    @Override
    public String toString() {
        Map<T, List<T>> sets = new HashMap<>();
        for (T t : mapper.keySet()) {
            T root = find(t);
            if (!sets.containsKey(root)) {
                sets.put(root, new ArrayList<>());
            }
            sets.get(root).add(t);
        }
        StringBuilder res = new StringBuilder();
        for (T present : sets.keySet()) {
            res.append(present);
            res.append(":");
            res.append(sets.get(present));
            res.append("\n");
        }
        return res.toString();
    }
}

结语

本篇使用类似树的结构来代表一个集合，透过一个森林来表示一个并查集，并加入两个操作优化机制（按秩合并+路径搜索），供大家参考。

除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog

标签：algorithm java 算法 数据结构 并查集 disjoint set

上一篇： 实验九 类与对象（一） 程序片段编程题 3. 菜单类的设计与实现

下一篇： AI开源评测基准AI-Rank，为开源建立标准

精华推荐