特征选择 Relief 方法
日期: 2020-12-12 分类: 跨站数据测试 722次阅读
1. 原理
该方法假设特征子集的重要性是由子集中的每个特征所对应的相关统计分量之和所决定的。
所以只需要选择前 k k k 个大的相关统计量对应的特征,或者大于某个阈值的相关统计量对应的特征即可。
2. 公式
2.1 二分类
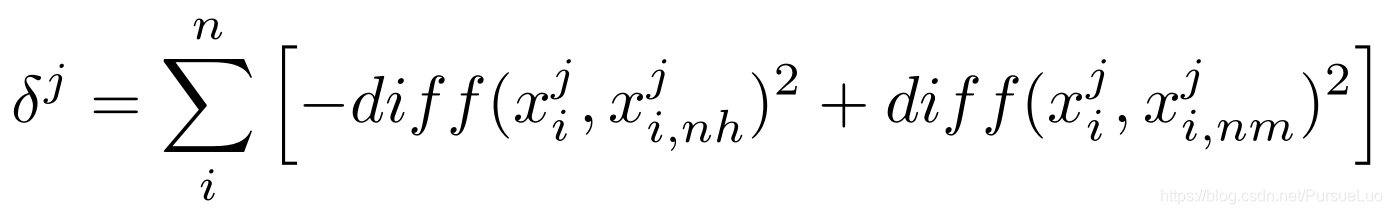
其中:
δ j \delta_j δj :属性 j j j 的相关统计量;
x i j x_i^j xij:样本 x i x_i xi 中属性 j j j 的值;
x i , n h j x_{i,nh}^j xi,nhj:样本 x i x_i xi 的 “猜中近邻” x i , n h x_{i,nh} xi,nh 中属性 j j j 的值;
x i , n m j x_{i,nm}^j xi,nmj:样本 x i x_i xi 的 “猜错近邻” x i , n m x_{i,nm} xi,nm 中属性 j j j 的值;
d i f f ( x i j , x i , n h j ) diff(x_i^j,x_{i,nh}^j) diff(xij,xi,nhj):样本 x i x_i xi 和 x i , n h x_{i,nh} xi,nh 在属性 j j j 上值的差异;
d i f f ( x i j , x i , n m j ) diff(x_i^j,x_{i,nm}^j) diff(xij,xi,nmj):样本 x i x_i xi 和 x i , n m x_{i,nm} xi,nm 在属性 j j j 上值的差异;
若属性值为离散型,则 d i f f diff diff 当且仅当属性值相等时为 0,否则为 1;若属性值为连续型,则 d i f f diff diff 表示为距离。
2.2 多分类
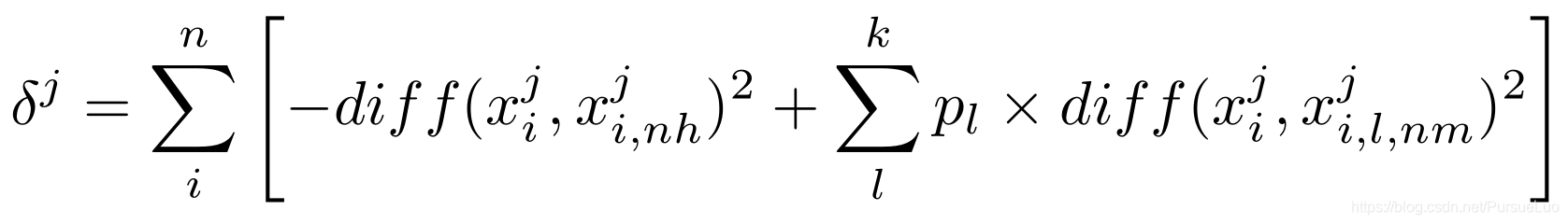
δ
j
\delta_j
δj :属性
j
j
j 的相关统计量;
x i j x_i^j xij:样本 x i x_i xi 中属性 j j j 的值;
x i , n h j x_{i,nh}^j xi,nhj:样本 x i x_i xi 的 “猜中近邻” x i , n h x_{i,nh} xi,nh 中属性 j j j 的值;
p l p_l pl:第 l l l 类样本的比例;
x i , l , n m j x_{i,l,nm}^j xi,l,nmj:样本 x i x_i xi 的第 l l l 类的 “猜错近邻” x i , l , n m x_{i,l,nm} xi,l,nm 中属性 j j j 的值;
d i f f ( x i j , x i , n h j ) diff(x_i^j,x_{i,nh}^j) diff(xij,xi,nhj):样本 x i x_i xi 和 x i , n h x_{i,nh} xi,nh 在属性 j j j 上值的差异;
d i f f ( x i j , x i , l , n m j ) diff(x_i^j,x_{i,l,nm}^j) diff(xij,xi,l,nmj):样本 x i x_i xi 和 x i , l , n m x_{i,l,nm} xi,l,nm 在属性 j j j 上值的差异;
3. 参考
除特别声明,本站所有文章均为原创,如需转载请以超级链接形式注明出处:SmartCat's Blog
精华推荐

