逻辑回归(Logistic Regression)
日期: 2019-05-08 分类: 跨站数据测试 435次阅读
一. 逻辑回归
在前面讲述的回归模型中,处理的因变量都是数值型区间变量,建立的模型描述是因变量的期望与自变量之间的线性关系。比如常见的线性回归模型:
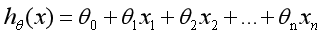
而在采用回归模型分析实际问题中,所研究的变量往往不全是区间变量而是顺序变量或属性变量,比如二项分布问题。通过分析年龄、性别、体质指数、平均血压、疾病指数等指标,判断一个人是否换糖尿病,Y=0表示未患病,Y=1表示患病,这里的响应变量是一个两点(0-1)分布变量,它就不能用h函数连续的值来预测因变量Y(只能取0或1)。
总之,线性回归模型通常是处理因变量是连续变量的问题,如果因变量是定性变量,线性回归模型就不再适用了,需采用逻辑回归模型解决。
逻辑回归(Logistic Regression)是用于处理因变量为分类变量的回归问题,常见的是二分类或二项分布问题,也可以处理多分类问题,它实际上是属于一种分类方法。
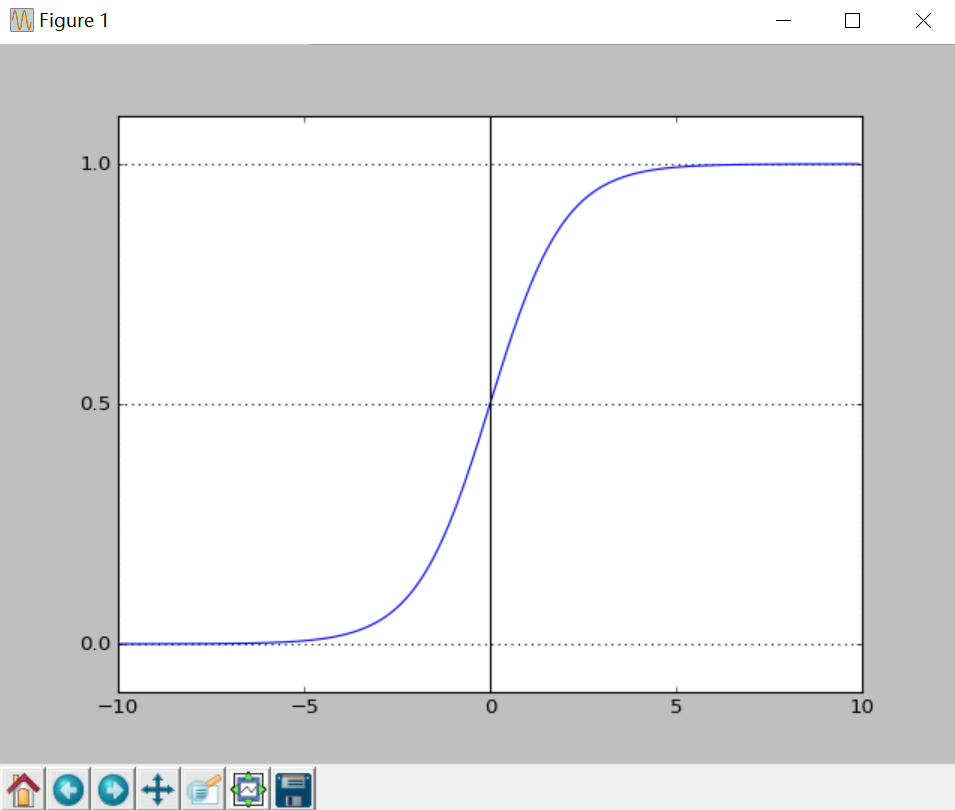
二分类问题的概率与自变量之间的关系图形往往是一个S型曲线,如图所示,采用的Sigmoid函数实现。
PS:如果你觉得这篇文章看起来稍微还有些吃力,或者想要系统地学习人工智能,那么推荐你去看床长人工智能教程。非常棒的大神之作。教程不仅通俗易懂,而且很风趣幽默。点击这里可以查看教程。
这里我们将该函数定义如下:
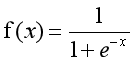
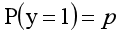
y=0的概率分布公式定义如下:
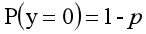
其离散型随机变量期望值公式如下:
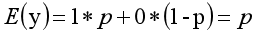
采用线性模型进行分析,其公式变换如下:
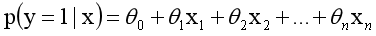
而实际应用中,概率p与因变量往往是非线性的,为了解决该类问题,我们引入了logit变换,使得logit(p)与自变量之
间存在线性相关的关系,逻辑回归模型定义如下:
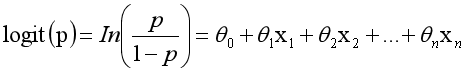
通过推导,概率p变换如下,这与Sigmoid函数相符,也体现了概率p与因变量之间的非线性关系。以0.5为界限,预
测p大于0.5时,我们判断此时y更可能为1,否则y为0。
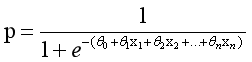
得到所需的Sigmoid函数后,接下来只需要和前面的线性回归一样,拟合出该式中n个参数θ即可。test17_05.py为绘
制Sigmoid曲线,输出上图所示。
-
import matplotlib.pyplot
as plt
-
import numpy
as np
-
-
def Sigmoid(x):
-
return
1.0 / (
1.0 + np.exp(-x))
-
-
x= np.arange(
-10,
10,
0.1)
-
h = Sigmoid(x)
#Sigmoid函数
-
plt.plot(x, h)
-
plt.axvline(
0.0, color=
'k')
#坐标轴上加一条竖直的线(0位置)
-
plt.axhspan(
0.0,
1.0, facecolor=
'1.0', alpha=
1.0, ls=
'dotted')
-
plt.axhline(y=
0.5, ls=
'dotted', color=
'k')
-
plt.yticks([
0.0,
0.5,
1.0])
#y轴标度
-
plt.ylim(
-0.1,
1.1)
#y轴范围
-
plt.show()
- 1
二. LogisticRegression回归算法
LogisticRegression回归模型在Sklearn.linear_model子类下,调用sklearn逻辑回归算法步骤比较简单,即:
(1) 导入模型。调用逻辑回归LogisticRegression()函数。
(2) fit()训练。调用fit(x,y)的方法来训练模型,其中x为数据的属性,y为所属类型。
(3) predict()预测。利用训练得到的模型对数据集进行预测,返回预测结果。
代码如下:
-
from sklearn.linear_model
import LogisticRegression
#导入逻辑回归模型
-
clf = LogisticRegression()
-
print clf
-
clf.fit(train_feature,label)
-
predict[
'label'] = clf.predict(predict_feature)
- 1
输出结果如下:
-
LogisticRegression(C=
1.0, class_weight=
None, dual=
False, fit_intercept=
True,
-
intercept_scaling=
1, max_iter=
100, multi_class=
'ovr', n_jobs=
1,
-
penalty=
'l2', random_state=
None, solver=
'liblinear', tol=
0.0001,
-
verbose=
0, warm_start=
False)
- 1
其中,参数 penalty 表示惩罚项( L1 、 L2 值可选。 L1 向量中各元素绝对值的和,作用是产生少量的特征,而其他特征
都是0,常用于特征选择;L2向量中各个元素平方之和再开根号,作用是选择较多的特征,使他们都趋近于0。); C
值的目标函数约束条件:s.t.||w||1<C,默认值是0,C值越小,则正则化强度越大。
2. 正则化选择参数:penalty
LogisticRegression和LogisticRegressionCV默认就带了正则化项。penalty参数可选择的值为"l1"和"l2".分别对应L1的正则化和L2的正则化,默认是L2的正则化。
在调参时如果我们主要的目的只是为了解决过拟合,一般penalty选择L2正则化就够了。但是如果选择L2正则化发现还是过拟合,即预测效果差的时候,就可以考虑L1正则化。另外,如果模型的特征非常多,我们希望一些不重要的特征系数归零,从而让模型系数稀疏化的话,也可以使用L1正则化。
penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择,如果是L2正则化,那么4种可选的算法{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}都可以选择。但是如果penalty是L1正则化的话,就只能选择‘liblinear’了。这是因为L1正则化的损失函数不是连续可导的,而{‘newton-cg’, ‘lbfgs’,‘sag’}这三种优化算法时都需要损失函数的一阶或者二阶连续导数。而‘liblinear’并没有这个依赖。
3. 优化算法选择参数:solver
solver参数决定了我们对逻辑回归损失函数的优化方法,有4种算法可以选择,分别是:
a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候,SAG是一种线性收敛算法,这个速度远比SGD快。关于SAG的理解,参考博文 除特别声明,本站所有文章均为原创,如需转载请以超级链接形式注明出处:SmartCat's Blog
精华推荐

