双目视觉之立体校正
日期: 2020-04-02 分类: 跨站数据测试 640次阅读
在本篇文章中,将根据上一篇文章得到的两个摄像机的相对位置进行图像的立体校正
-
引言
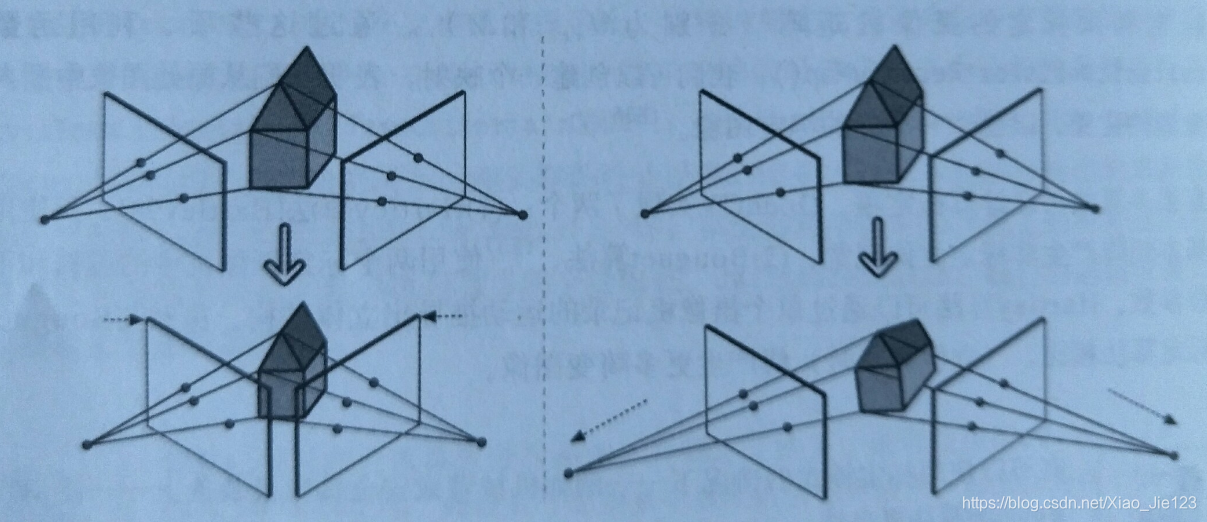
当两个像平面式完全行对准的,计算立体视差是最简单的。但是两台摄像机几乎不可能有准确的共面和行对准成像平面,完美的对准结构在真实的立体系统中几乎不存在。因此,立体校正的目的是对两台摄像机的图像平面重投影,使得它们精确落在同一个平面上,而且图像的行完全地对准到前向平行的结构上。要保证两个摄像机的图像在校正之后是对准的,使得后续的立体匹配更可靠,计算更可行。因为只在图像的一行上面搜索另一图像的匹配点能够可靠性和算法效率。让每个图像平面都落在一个公共成像面上并水平对准的结果是极点都位于无穷远。即一幅图像上的投影中心成像与另一个像平面平行。但是由于可选择的前向平行平面个数是有限的,因此需要更多的约束,包括视图重叠最大化和畸变最小化。
对准后的两个图像平面后的结果有八项,左右摄像机各四项(畸变向量、旋转矩阵、校正后的摄像机矩阵、未校正后的摄像机矩阵)
-
计算校正项的两种算法
- Hartley算法(使用基本矩阵来生成非标定立体视觉)非标定的立体校正
- Hartley算法目的是找到将极点映射到无穷远处的单应矩阵,同时使两幅立体图像之间的计算误差最小化,实现这种算法要通过匹配两幅图像之间的对应点实现,通过这种方法,就可以绕过计算两个摄像机的摄像机内参数,因为这样的内参数信息隐含在匹配点之中
- Hartley算法的优缺点
1) 优点:通过观察场景中的点简便地进行线粒体标定
2) 缺点:场景图像的比例未知
立体重建具有非唯一性,如果物体的大小未知,那么不同大小物体可以看起来相同,这取决于它们与摄像机之间的距离,如果摄像机参数未知,那么不同投影可以看起来相同—例如,在焦距和主点不同的情况下 - 算法描述(假设已知基本矩阵)
- 使用基本矩阵,通过关系
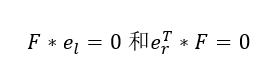
计算左右两个极点 - 先求第一个单应矩阵Hr ,他将右极点映射到无穷远(1,0,0)T处的二维齐次点。由于一个单应矩阵有7个约束,使用其中的三个进行无穷远处的映射,剩下的四个自由度进行选择矩阵Hr ,这四个自由度大都容易导致混乱,因为Hr 的大多数选择将导致高度扭曲的图像。为了找到一个较好的Hr ,我们在图像中选择一点产生扭曲的可能性最小,仅允许刚性旋转和平移。对于这一点的一个合理的选择是图像原点,进一步假设极点er = (k,0,1)T落在x轴上,而下述矩阵就会实现将这样的一个点映射到无穷远。
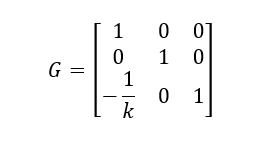
- 在有图像上选择一个感兴趣的点(这里选择原点),计算点到图像原点的平移矩阵T和将极点指向(er )T = (k,0,1)的旋转矩阵R,则需要的单应性矩阵就是Hr = GRT。
- 接下来就是搜索匹配的单应矩阵Hl ,他将左极点发送到无穷远,并保证两幅图像的行对准。通过步骤2中的三个约束可以容易地将座机带你转到无穷远。为了能够行对准,依靠地依据就是行对准使两幅图像地所有匹配点据距离和最小。也就是说,搜寻地Hl ,使得左右匹配点地总的视差最小,也就是
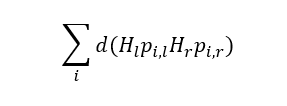
最小,则这两个单应性矩阵就定义了立体校正。
- 使用基本矩阵,通过关系
- Bouguet算法(使用两台摄像机的旋转和平移参数)标定立体校正
- 算法概览
给定立体图像间地旋转矩阵和平移矩阵(R,T),Bouguet的算法目的是使两图像中的每一幅重投影次数最小化,同时使得观测面积最大化。为了使图像重投影畸变最小,将右摄像机图像平面旋转到左摄像机图像平面的旋转矩阵R被分离成两部分,称左右摄像机的两个合成旋转矩阵r1和r2。每个摄像机都旋转一半,这样地旋转可以让摄像机共面但是行不对准。为了计算将左摄像机极点变换到无穷远并使极线水平对准地Rrect。创建一个由极点el方向开始的旋转矩阵。 - 算法描述
让主点(cx,cy)作为左图像的原点,极点的方向就是两台摄像机投影中心之间的平移向量方向:

下一个向量e2必须与e1正交,因此最好的选择就是选择与主光线正交的方向(通常沿着图像平面)。这可以通过计算e1和主光线方向的叉积来得到,然后将他归一化到单位向量:
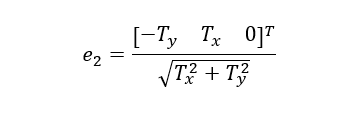
这样就可以求出第三个向量e3,它可以通过e1和e2的叉积得到:
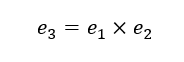
此时,将左摄像机的极点转换到无穷远处的矩阵如下:
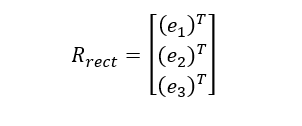
这个矩阵将左图像绕着投影中心旋转,使得极线变成水平,并且极点在无穷远处。两台摄像机的行对准通过下述公式实现:
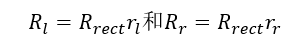
计算校正后的左右摄像机矩阵Mrect_l和Mrect_r,但是与投影矩阵Pl和Pr一起返回:
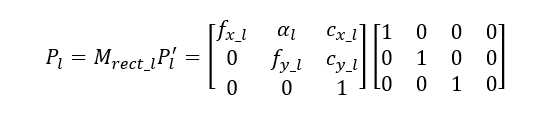
和
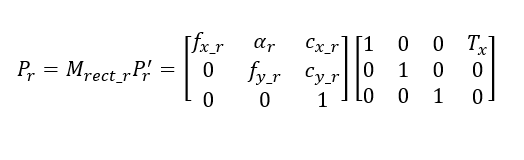
其中αl 和αr 是像素畸变比例,在现代计算机中几乎等于0。投影矩阵将齐次坐标中的三维点转换成齐次坐标系下的二维点:
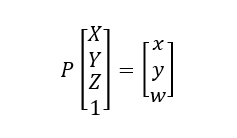
则屏幕坐标为(x/w,y/w)。如果给定屏幕坐标和摄像机内参数矩阵,二维点同样可以重投影到三维中,重投影矩阵如下:

上述公式中,除cx’外的所有参数都是来自左图像,cx’是主点在右图像上的x坐标。如果主光线在无穷远处相交,那么cx = cx’,并且游侠的项为0。给定一个二维其次点和其关联的视差d,可以将此点投影到三维中:
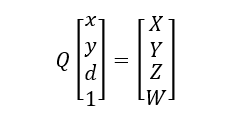
因此三维坐标就是(X/W,Y/W,Z/W),在这里d还是一个未知数,在下节将会进行介绍
- 算法概览
- Hartley算法(使用基本矩阵来生成非标定立体视觉)非标定的立体校正
-
由上面三篇文章就可以得到如下效果:
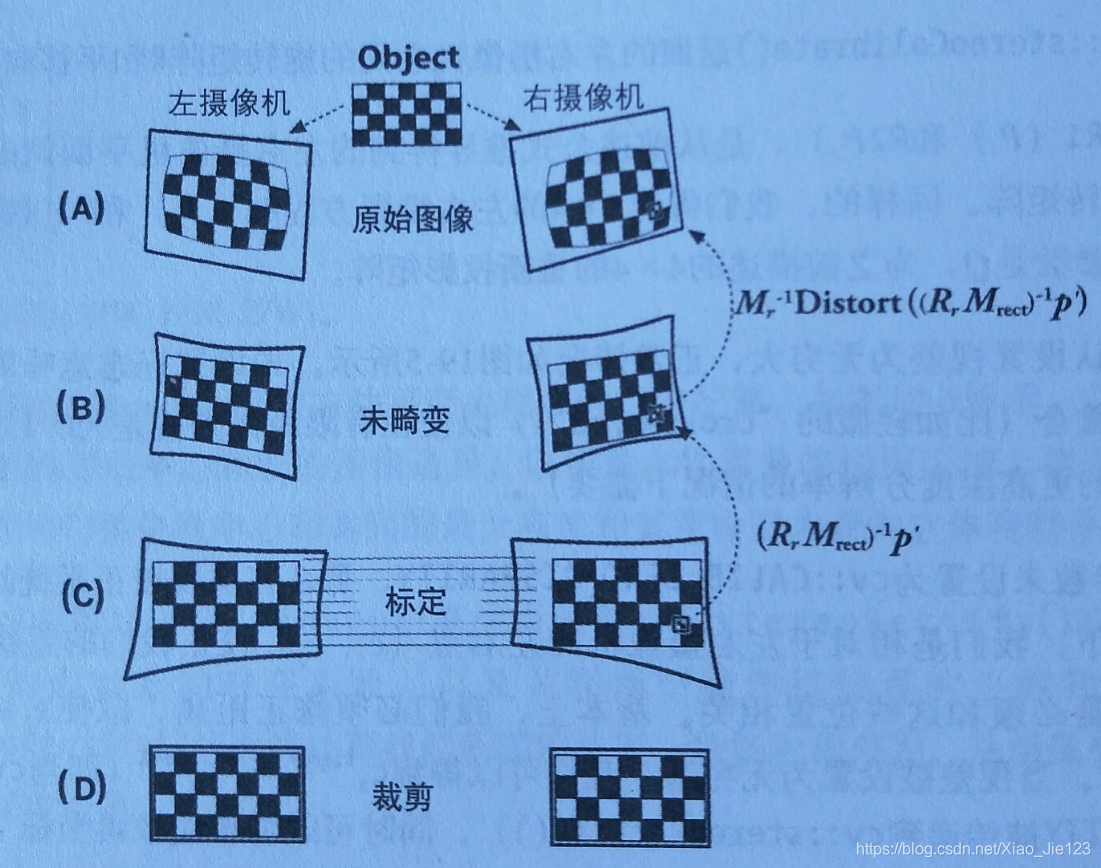
参考文献:Adrian Kaehler,Gary Bradski,Learning Opencv3[M],清华大学出版社,2018.7
下面的是笔者的微信公众号,欢迎关注,会持续更新c++、python、tensorflow、机器学习、深度学习、计算机视觉等系列文章,公众号中内含300+本pdf电子书籍,肯定有你需要的一本,关注公众号即可领取哦。

如果你对JAVA方面感兴趣,可以关注下面JAVAERS公众号,陪你一起学习,一起成长,一起分享JAVA路上的诗和远方。在公众号里面都是JAVA这个世界的朋友,公众号每天会有技术类文章,面经干货,也有进阶架构的电子书籍,如Spring实战、SpringBoot实战、高性能MySQL、深入理解JVM、RabbitMQ实战、Redis设计与实现等等一些高质量书籍,关注公众号即可领取哦。

除特别声明,本站所有文章均为原创,如需转载请以超级链接形式注明出处:SmartCat's Blog
精华推荐

