当前位置：首页 >跨站数据测试

利用哈夫曼树进行编码压缩

日期： 2019-06-14 分类：跨站数据测试 337次阅读

文章目录

前言
题目：利用哈夫曼编码进行字符串压缩
算法步骤
示例
总结

前言

哈夫曼树是上世纪50年代由哈夫曼提出的一种完全二叉树，能够用于很多算法当中。比较经典应用之一的就是利用哈夫曼树进行数据压缩。网上相关文章很多，请先自行查询相关算法的文章进行预习。

题目：利用哈夫曼编码进行字符串压缩

算法输入：一个字符串
算法内容：利用哈夫曼树对出现频率高的字符用更短编码的方式达到压缩字符串长度的目的。
算法输出：压缩后的一串二进制位

算法步骤

算法总共分为六步，每一步有不同的输入和输出。整体数据结构并不是在一开始就完全建立，每一步会根据需求不断地添加和修改数据结构，使数据结构达到最终的需求，并完成压缩编码。

1.统计字符串中每个字符出现的次数

【输入】一个字符串，如 s = “aaaabbbccd”
【输出】一个 int[] 数组，表示字母出现的概率
【说明】输入字符串，第一位的内容并不是固定的，可以是以上的a,b,c,d，也可以是其他内容。由于1个字符只有256种可能用二进制表示为：

二进制       十六进制     十进制 
00000000     00          0
00000001     01          1
00000010     02          2
...
11111110     FE        254
11111111     FF        255

所以，我们使用一个长度为256的整型数组来表示即可，如int[] occ = new int[256] 其中，第i个元素的值表示 (char)i 的出现次数。如 occ[65] 表示 (char)65 ，即字符 A 的出现次数。

2.根据字符出现次数生成一序列树的节点

【输入】概率数组
【输出】Node链表
【说明】首先，建立节点类Node（可直接将当前类更名为Node），然后为节点添加以下属性

public byte data;         // 对应的字符元素
public int occ;           // 出现次数
public int total;         // 总次数
public double probility;  // 概率
public String code = "";  // 编码
public Node left;         // 左子树
public Node right;        // 右子树

再添加以下构造函数以方便操作

public Node(int data, int occ, int total){
	this.data = (byte)data;
	this.occ = occ;
	this.total = total;
}

再添加以下两个函数用于输出。

	@Override
	public String toString() {
		return String.format(" %c\t%d\t%d\t%8.3f%%\t%s", data, occ, total, probility * 100, code);
	}

	public static void show(ArrayList<Node> nodes) {
	System.out.println("data\tocc\ttotal\tprobility\tcode");
		nodes.forEach(System.out::println);
	}

3.利用这些节点创建哈夫曼树

【输入】Node链表
【输出】哈夫曼树的根，即1个Node对象
【说明】如下图所示，哈夫曼树的生成有在下两个步骤：

根据出现次数（或概率）对Node链表排序
建立新节点，然后将链表最左边两个节点分别作为新节点的左右树，最后添加新节点至链表中
如果链表中元素个数等于1则结束，否则回到第1步

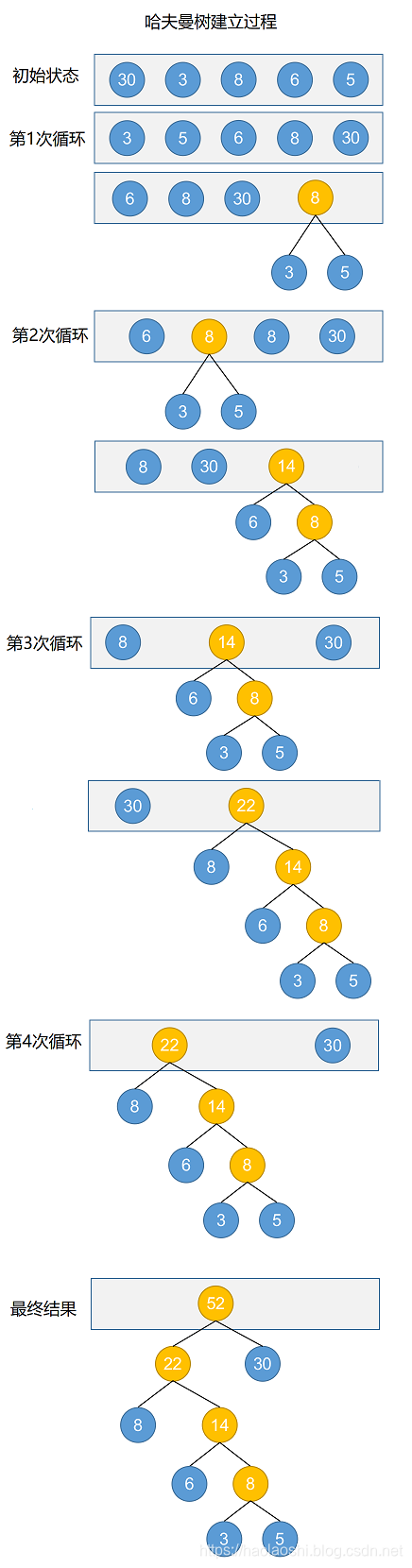
在这里插入图片描述

示意图说明：在以上的示意图上，圆代表节点，节点中的数字代表出现次数，方框代表Node链表。示意图以出现次数为参考值，使用出现次数为[3，5，6，8，30]的5个节点，演示了哈夫曼树的从一个Node链表至一颗树的生成过程。注：使用出现次数和使用概率结果是一样的。

为了方便操作，添加以下内容以实现Node链表的排序

// 1. 在类上添加 Comparalble 接口，如下所示
public class Node implements Comparable<Node> {

// 2. 在Node类中实现 compareTo(Node other)方法
@Override
public int compareTo(Node other) {
	return this.probility == other.probility ? 0 : (this.probility < other.probility ? -1 : 1);
}

// 3. 使用Collections.sort(ndoes)进行调用

在创建树时，添加以下构造函数，以方便Node对象的创建

public Node(Node left, Node right) {
	this.left = left;
	this.right = right;
	this.probility = left.probility + right.probility;
	left.code = "0";
	right.code = "1";
}

4.利用哈夫曼树生成每个字符的编码

【输入】未编码的哈夫曼树的根
【输出】带有编码信息的节点列表
【说明】根据上一步生成的哈夫曼树，生成每个字符的编码

示意图
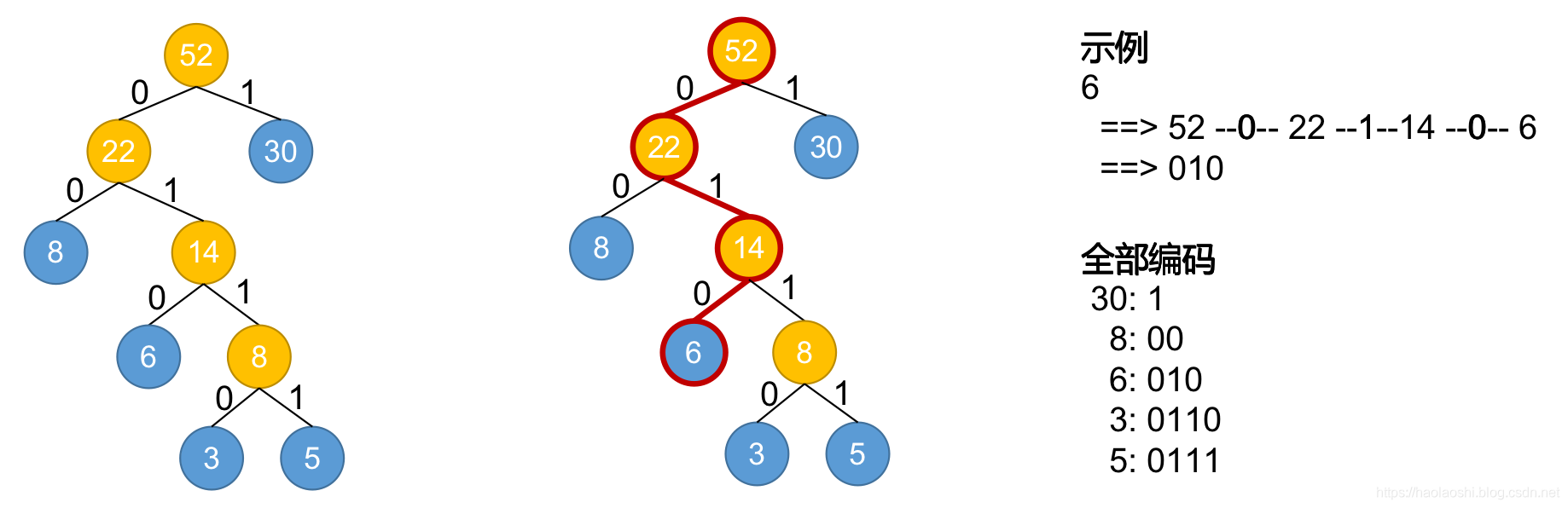
在这里插入图片描述
示意图说明：在以上的示意图中，我们通过自上向下的遍历，实现不每个字符的编码。如图所示，蓝色节点是数据节点，即需要编码的节点，而橙色的是我们添加的节点，不需要进行编码。左图为已经生成但是未编码的哈夫曼树。中间图表示对6进行编码的过程，右侧上是对6编码的过程，右侧下为所有元素编码的最终结果。

实现方法提示：
利用Queue来实现逐层递归编码。在每一层中，每个节点的编码等于其编码加上其父节点的编码。自顶向下进行遍历，直到所有节点都进行编码计算。

5.创建用于编码的字典

【输入】带有编码的Node链表
【输出】字符串编码数组
【说明】根据每个Node中带有的code，生成一个长度为256的字符串数组，第i个元素表示第i个字符的编码。

6.生成压缩后的字符串编码

【输入】原始数据+编码字符串数组
【输出】编码完成的字符串。
利用编码字符串数组对原始数据进行编码，从而生成编码后的只包括0和1的字符串。

示例

输入字符串：aaaabbbccd，长度为 10 个字节。
压缩后内容：0000101010111111110 长度为19位，可以用 3个字节表示。

压缩前后可以看到，原长度为10字节减少至3字节，压缩率为 70%。

附：中间各字符的概率和编码信息

data	occ	  total   probility  code
 a	    4      10	  40.000%  	 0
 b	    3      10	  30.000%	 10
 d	    1      10	  10.000%	 110
 c	    2      10	  20.000%	 111