说明

'''
这是《数据结构与算法 Python 语言实现》 （古德里奇）版，每一章书后习题和自己的一些解答，、
我已经买了这本书，因为想在看完每一章后，完成习题，所以记录下来！
这篇文章是第一章的习题内容！因为题目太长，懒得自己书写，我拍下了习题，并且直接用截图作为题目！
'''

巩固题

编写一个Python函数 is_multiple(n, m)，用来接收两个整数值 n 和 m，
如果 n 是 m 的倍数，即存在整数 i 使得 n = mi，那么函数返回 True，否则返回 False

def is_multiple(n, m):
    return (n % m == 0)

print(is_multiple(4, 2))

不能用乘法、除法、取余的操作来判断传入的数是偶数（返回Ture）

def is_even(k):
    return (k & 1 == 0)


print(is_even(5))

# 用减法？
def is_even(k):
    k = abs(k)
    while k > 1:
        k = k - 2
    return (k == 0)


print(is_even(10))

传入一个序列，找出其中最大和最小的值，并以一个长度为2的元组形式返回，不能使用max和min

def minmax(data):
    small = big = data[0]  # 假设非空
    for val in data:
        if val < small:
            small = val
        if val > big:
            big = val
    return small, big


print(minmax([1, 2, 5, 8, 6])) # 结果：(1,8)

接受一个正整数n，返回1~n的平方和

def sum_of_squares(n):
    total = 0
    for j in range(1, n + 1):
        total += j * j
    return total


print(sum_of_squares(5)) # 55

# 用推导式来写
def sum_of_squares(n):
    return sum(j * j for j in range(1, n + 1))


print(sum_of_squares(5)) # 55

接受一个正整数n，返回1~n中奇数的平方和

def sum_of_squares(n):
    total = 0
    for j in range(1, n + 1, 2): # 隔两个取一个，从1开始数
        total += j * j
    return total


print(sum_of_squares(5))

def sum_of_squares(n):
    return sum(j * j for j in range(1, n + 1, 2))


print(sum_of_squares(5))

li = [1, 2, 5, 6, 8]
print(len(li))  # 5

print(li[-4])  # 2

print(li[len(li)+(-4)]) # 2

索引规律为：负值+序列长度 即是： k+n

# 虽然很简单，但是“前开后闭”很容易错
range(50,81,10)

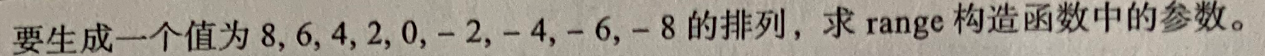
for i in range(8, -10, -2):
    print(i, end=" ") 

def get_num(n):
    return [2 ** i for i in range(n)]


print(get_num(9))

import random

def choice(data):
    return data[random.randrange(len(data))]


print(choice([1, 2, 3, 4])) # 结果是从列表中随机选择一个数

创新题

def has_odd_pair(data):
    count = 0
    for j in range(len(data)):
        if data[j] % 2 == 1:
            count += 1
            if count == 2:
                return True
    return False


print(has_odd_pair([5, 1, 3, 6]))

# 乘积要是奇数，奇数个数必须至少有两个

# 让后一个数和前面的数一次进行比较，类似冒泡排序
def distinct(data):
    for k in range(1, len(data)):
        for j in range(k):
            if data[j] == data[k]:
                return False
    return True  


print(distinct([1, 3, 6, 5, 4])) # True
print(distinct([1, 3, 6, 3, 4])) # False

lis=[i*(i+1) for i in range(0,10)]
print(lis)

Alphabet = [chr(k) for k in range(97, 123)]

print(Alphabet)

# 法二

Alphabet = list(map((lambda x: chr(ord('a') + x)), range(26)))
print(Alphabet)

'''
Hint:
Consider randomly swapping an element to the first position, 
then randomly swapping a remaining element to the second position,
and so on.
'''

# 翻转 reversed 列表才有
lines = []
while True:
    try:
        single = input()
        lines.append(single)
    except EOFError: 
    # 出现“EOFError Python”，就意味着发现了一个不期望的文件尾，而这个文件尾通常是Ctrl-d引起的
        break  
print('\n'.join(reversed(lines)))

'''
fjsd
fasdf
asdfwe
^D # 结束
asdfwe
fasdf
fjsd
d
'''

return [a[k]*b[k] for k in range(n)]

def get_num(a, b):
    import numpy as np
    return np.array(a) * np.array(b)
    
a = [1, 2, 3]
b = [4, 5, 6]
print(get_num(a ,b))

def get_erro(data, i):
   try:
       return data[i]
   except IndexError:
       print("Don't try buffer overflow attacks in Python!")

data = [1, 2, 3 ]
get_erro(data, 3)

def num_vowels(text):
    total = 0
    for ch in text.lower():
        if ch in 'aeiou':
            total += 1
    return total


print(num_vowels("aEcdefjdaeo"))

# 法一 
string = "Let's try, Mike."
ret = string.split(" ")

for aph in ret:

    res = ""
    for el in aph:
        if ord(el.lower()) in range(97, 123): # 用字母对应的码值来筛选
            res += el
    print(res, end=" ")

# 法二：正则表达式
import re

string = "Let's try, Mike."
res = re.sub("[.',]", "", string)
print(res)

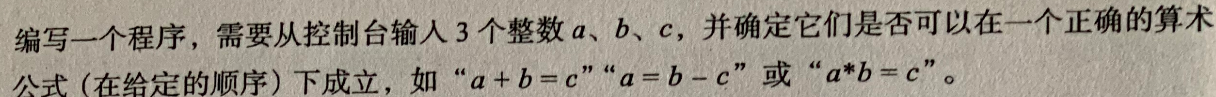
def get_num():
    li = []
    while True:
        temp = int(input("please enter three num:"))
        li.append(temp)
        if len(li) == 3:
            break
    a, b, c = li[0], li[1], li[2]
    if (a + b == c) or (a == b - c) or (a * b == c):
        return True
    else:
        return False


print(get_num())

def factors(n):
    k = 1
    temp = []
    while k * k < n:
        if n % k == 0:
            yield k
            temp.append(n // k)
        k += 1
    if k * k == n:
        yield k
    for item in temp[::-1]:
        yield item


res = list(factors(100))
print(res) # [1, 2, 4, 5, 10, 20, 25, 50, 100]

# 法一
def norm(v, p=2):
    import math
    return math.sqrt(sum(pow(x, p) for x in v))


v = [3, 4]
print(norm(v)) # 5.0

# 法二
def norm(v, p=2):
    temp = sum(val ** p for val in v)
    return temp ** (1 / p)


v = [3, 4]
print(norm(v)) # 5.0

项目

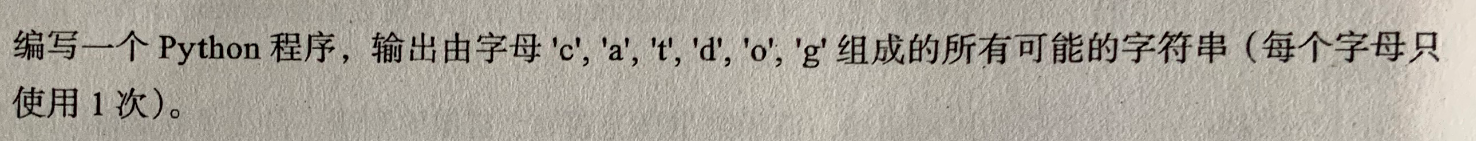
这道题解法有很多（实质：全排列）

递归思路

# 原书本中做法：递归
def permute(bag, permutation):
    # When the bag is empty, a full permutation exists
    if len(bag) == 0:
        print(''.join(permutation))
    else:
        # For each element left in the bag
        for k in range(len(bag)):
            # Take the element out of the bag and put it at the end of the permutation
            permutation.append(bag.pop(k))
            # Permute the rest of the bag (recursively)
            permute(bag, permutation)
            # Take the element off the permutation and put it back in the bag
            bag.insert(k, permutation.pop())


permute(list('catdog'), [])

'''
原书中用的是递归方法，而且还用了列表的方法，更加简便了
'''
# 详细来解答下思路过程

'''
例如对[1,2,3]进行全排：

固定数组的第一个元素list[0]，然后对之后的元素list[1:]进行递归全排列，得到list[1:]的全排列之后，
遍历list[1:]的全排列结果，将list[0]分别插入每一个结果中的每一个位置。
如数组[1,2,3]，固定1，对[2,3]全排列，得到结果[2,3]和[3,2]。
将1插入每一个结果的每一个位置，即对于[2,3]，将1插入之后得到[1,2,3]、[2,1,3]、[2,3,1];
对于[3,2]，将1插入之后得到[1,3,2]、[3,1,2]、[3,2,1]
'''
# 第一种递归做法
def full_permutation(list):
    if list == None: # 递归出口
        return None
    if len(list) == 1:  # 因为是从list[1]处开始递归的，若len(list)<=1，list会越界
        return [list]
    res = []
    left = list[0]
    right = full_permutation(list[1:])
    for i in right:
        for j in range(len(i) + 1):
            res.append(i[:j] + [left] + i[j:])
    return res


print(full_permutation([1, 2, 3]))


# 第二种递归做法
# 摘自：https://blog.csdn.net/ggdhs
 除特别声明，本站所有文章均为原创，如需转载请以超级链接形式注明出处：SmartCat's Blog